Các đường cong kinh tế học: Đường cong Lorenz

E-mail | Bản in | Lưu xem sau

Đường cong Lorenz là một loại đồ thị dùng để biểu diễn mức độ bất bình đẳng trong phân phối. Nó được phát triển bởi Max.O.Lorenz từ năm 1905 để thể hiện sự phân phối thu nhập. Đường cong Lorenz là sự biểu diễn bằng hình học của hàm phân bố tích lũy, chỉ ra quan hệ giữa tỷ lệ phần trăm của một giá trị thể hiện qua trục tung với tỷ lệ phần trăm của một giá trị khác thể hiện qua trục hoành. Đường cong Lorenz thường được sử dụng trong việc nghiên cứu sự phân bố thu nhập, chỉ ra tỷ lệ phần trăm số hộ gia đình hay dân số trong tổng số và tỷ lệ phần trăm thu nhập của họ trong tổng thu nhập.

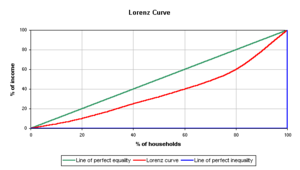
Tỷ lệ phần trăm cộng dồn số hộ gia đình được thể hiện trên trục hoành, và tỷ lệ phần trăm cộng dồn thu nhập thể hiện trên trục tung.

Đường màu xanh lá cây hợp với trục hoành thành một góc 45° gọi là đường bình đẳng tuyệt đối. Mỗi điểm trên đường này thể hiện tỷ lệ phần trăm số hộ gia đình đúng bằng tỷ lệ phần trăm thu nhập.

Đường màu xanh da trời được gọi là đường bất bình đẳng tuyệt đối. Mỗi điểm trên đường này thể hiện tỷ lệ phần trăm số hộ gia đình không có thu nhập hoặc tỷ lệ phần trăm số hộ gia đình chiếm toàn bộ tổng thu nhập.

Đường cong Lorenz luôn luôn bắt đầu từ điểm (0,0) và kết thúc tại điểm (1,1). Nó không thể nằm phía trên đường bình đẳng tuyệt đối, cũng không thể nằm phía dưới đường bất bình đẳng tuyệt đối. Một đường Lorenz điển hình là đường lõm hướng về gốc (0,0). Một điểm bất kỳ trên đường Lorenz cho biết tỷ lệ % cộng dồn của nhóm dân cư nghèo nhất nhận được bao nhiêu % tổng thu nhập. Như vậy đường Lorenz là cách biểu hiện trực quan của sự bất bình đẳng trong phân phối thu nhập, nó càng lõm thì mức độ bất bình đẳng trong phân phối thu nhập càng cao.

Hạn chế của đường Lorenz

Đường cong Lorenz của 3 quốc gia X, Y, Z

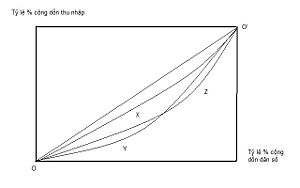
Mặc dù biểu hiện một cách trực quan, dễ thấy mức độ bất bình đẳng trong phân phối thu nhập nhưng bản thân đường cong Lorenz không phải là cách đánh giá định lượng về sự bất bình đẳng trong phân phối thu nhập. Mặt khác, kể cả khi so sánh đường Lorenz giữa các quốc gia một cách trực quan, trong nhiều trường hợp cũng không thể đưa đến kết luận quốc gia nào có mức độ bất bình đẳng cao hơn. Khi các đường Lorenz không cắt nhau thì đường nào lõm hơn sẽ thể hiện mức độ bất bình đẳng lớn hơn nhưng khi chúng cắt nhau thì không thể đưa ra kết luận được. Ví dụ như trong hình bên, nhìn đường Lorenz của ba quốc gia X, Y, Z ta chỉ có thể biết Y và Z có mức độ bất bình đẳng cao hơn X còn giữa Y và Z thì không biết được quốc gia nào có mức độ bất bình đẳng lớn hơn.

Để khắc phục nhược điểm này, người ta thường sử dụng hệ số Gini (do nhà thống kê học người Ý Corrado Gini xây dựng) là tỷ lệ phần trăm giữa diện tích của vùng nằm giữa đường bình đẳng tuyệt đối và đường cong Lorenz với diện tích của vùng nằm giữa đường bình đẳng tuyệt đối và đường bất bình đẳng tuyệt đối. Giá trị của hệ số Gini nằm trong khoảng từ 0 đến 1, giá trị càng cao thì mức độ bất bình đẳng càng lớn. Những quốc gia có hệ số Gini từ 0,5 trở lên thì được coi là có mức độ bất bình đẳng cao còn trong khoảng 0,2 đến 0,35 thì phân phối tương đối công bằng.

(Theo Bách khoa toàn thư mở Wikipedia)